DS - BST
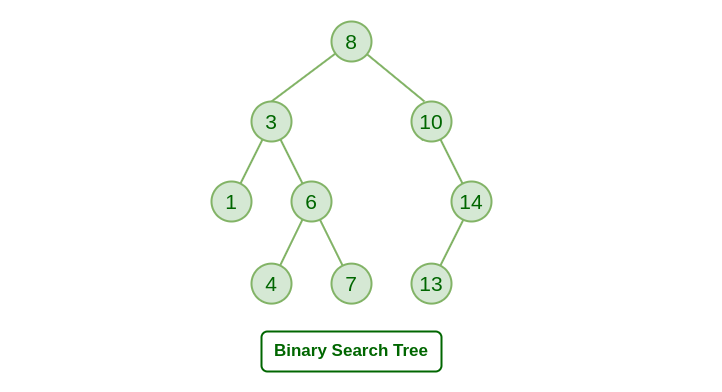
Binary Search Tree (BST) in Data Structures
A Binary Search Tree (BST) is a special kind of binary tree where each node follows a specific ordering property:
- Left Subtree: Contains nodes with values less than the node’s value.
- Right Subtree: Contains nodes with values greater than the node’s value.
- Both left and right subtrees must also be binary search trees.
🔍 Properties of BST
- Binary Tree Structure: Each node has at most two children.
- Ordered: Left child < Parent < Right child
- No Duplicate Values: Typically, BSTs don’t allow duplicate elements.
⚙️ Operations on a BST
| Operation | Time Complexity | Description |
|---|---|---|
| Search | O(log n) (Balanced) / O(n) (Unbalanced) | Find if an element exists. |
| Insert | O(log n) (Balanced) / O(n) (Unbalanced) | Add a new element. |
| Delete | O(log n) (Balanced) / O(n) (Unbalanced) | Remove an element. |
| Traversal | O(n) | Visit all nodes (In-order, Pre-order, Post-order). |
🔗 Types of Traversal in BST
In-order (Left, Root, Right):Returns elements in sorted order.Pre-order (Root, Left, Right):Useful for copying the tree.Post-order (Left, Right, Root):Useful for deleting the tree.
💻 Implementation of a Binary Search Tree
1#include <stdio.h>
2#include <stdlib.h>
3
4struct BinaryTreeNode
5{
6 int key;
7 struct BinaryTreeNode *left, *right;
8};
9
10struct BinaryTreeNode *newNodeCreate(int value)
11{
12 struct BinaryTreeNode *temp = (struct BinaryTreeNode *)malloc(
13 sizeof(struct BinaryTreeNode));
14 temp->key = value;
15 temp->left = temp->right = NULL;
16 return temp;
17}
18
19struct BinaryTreeNode *
20insertNode(struct BinaryTreeNode *node, int value)
21{
22 if (node == NULL)
23 {
24 return newNodeCreate(value);
25 }
26 if (value < node->key)
27 {
28 node->left = insertNode(node->left, value);
29 }
30 else if (value > node->key)
31 {
32 node->right = insertNode(node->right, value);
33 }
34 return node;
35}
36
37void postOrder(struct BinaryTreeNode *root)
38{
39 if (root != NULL)
40 {
41 postOrder(root->left);
42 postOrder(root->right);
43 printf(" %d ", root->key);
44 }
45}
46void inOrder(struct BinaryTreeNode *root)
47{
48 if (root != NULL)
49 {
50 inOrder(root->left);
51 printf(" %d ", root->key);
52 inOrder(root->right);
53 }
54}
55
56void preOrder(struct BinaryTreeNode *root)
57{
58 if (root != NULL)
59 {
60 printf(" %d ", root->key);
61 preOrder(root->left);
62 preOrder(root->right);
63 }
64}
65int main()
66{
67 struct BinaryTreeNode *root = NULL;
68
69 root = insertNode(root, 50);
70 insertNode(root, 30);
71 insertNode(root, 20);
72 insertNode(root, 40);
73 insertNode(root, 70);
74 insertNode(root, 60);
75 insertNode(root, 80);
76 postOrder(root);
77 printf("\n");
78
79 preOrder(root);
80 printf("\n");
81
82 inOrder(root);
83 printf("\n");
84 return 0;
85}
✅ Advantages of a Binary Search Tree
- Efficient searching, insertion, and deletion when the tree is balanced.
- Provides sorted data through in-order traversal.
- Can be extended to more advanced trees (e.g., AVL Tree, Red-Black Tree).
❌ Disadvantages of BST
- Performance degrades to O(n) if the tree becomes unbalanced (like a linked list).
- Requires self-balancing (AVL, Red-Black) for consistently good performance.
🔄 Applications of BST
- Searching and sorting operations
- Implementing associative arrays
- In-memory data structures like sets and maps
- Used in databases for indexing