Token Embeddings (Data Preprocessing)

🧠2.Token Embeddings in LLMs
They’re also often called vector embeddings or word embeddings.
🔤 From Tokens to Token Embeddings
Before a model can “read” anything, it first breaks text into smaller chunks called tokens.
Each token is then assigned a unique token ID, a simple integer from the vocabulary.
For example:
| Text | Tokens | Token IDs |
|---|---|---|
| "The cat dog" | ["The", "cat", "dog"] | [101, 207, 450] |
But these IDs — 101, 207, 450 — don’t carry any meaning.
They’re just arbitrary numbers, these ids dosent carry any meaninng or correlation between the words, for eg cat and dog are both animals and have many features in common but wer're not able to get it with these token ids.
So, the next step — Step 3 in the text-to-model pipeline — is to convert these token IDs into token embeddings, which are numerical vectors that represent the meaning of each token.
These vectors are what actually get fed into the GPT model.
🌌 How Token Embeddings caputre the SEMANTIC MEANING
Token embeddings are important because they capture the semantic meaning of words using vectors.
These vectors are multi-dimensional vectors.
Instead of representing each word as an isolated symbol (token ids), embeddings represent them as points in a high-dimensional space, where words with similar meanings are placed close together.
Understanding Embedding Meaning with an Example
To understand how embeddings capture meaning, imagine that each dimension in the embedding vector represents a certain feature or property — like “has a tail,” “is edible,” or “is an animal.”
Each token (like cat, dog, or apple) can then be represented by a set of values along these dimensions.
| Feature / Dimension | Cat | Dog | Apple |
|---|---|---|---|
| Has a tail | 0.9 | 0.95 | 0.0 |
| Is an animal | 0.88 | 0.93 | 0.0 |
| Is edible | 0.1 | 0.05 | 0.95 |
| Is pet | 0.85 | 0.9 | 0.0 |
| Is fruit | 0.0 | 0.0 | 0.98 |
Here, you can see that cat and dog have similar values for features like “has a tail” and “is an animal,” meaning their vectors are close in the embedding space.
Meanwhile, apple has high values in dimensions like “is edible” and “is fruit,” placing it far away from the animal-related words.
These numerical values form the embedding vectors for each word — and this is what the model actually uses to understand relationships and meaning.
So, instead of just token IDs (like 101 or 205), the model works with vectors of learned features that reflect real-world similarities.
❌ Why Not One-Hot Encoding?
Before embeddings, a common way to represent words was one-hot encoding — where each token is a vector full of zeros with a single 1 marking its position in the vocabulary.
Example for a 5-word vocabulary:
| Token | One-Hot Vector |
|---|---|
| cat | [1, 0, 0, 0, 0] |
| dog | [0, 1, 0, 0, 0] |
| car | [0, 0, 1, 0, 0] |
While simple, this has two major problems:
- Each vector is very sparse (mostly zeros).
- There’s no sense of similarity — “cat” and “dog” are as different as “cat” and “car.”
That means one-hot encoding can’t capture semantic relationships or meaning between words.
Token embeddings fix this by using dense vectors where numbers can vary continuously — allowing relationships to emerge naturally during training.
in easy wods - Unlike one-hot encoding, where values are only 0 or 1 and say nothing about how words are related, vector embeddings use continuous values with varying magnitudes, allowing the model to understand how similar or different words are based on the strength of these values across dimensions.
🧮 Embedding Layer
In models like GPT, token embeddings are learned through an embedding layer, which is a type of lookup table that maps each token ID to its dimensions.
🧠 GPT’s Embedding Dimensions
GPT models have a large number of tokens and a fixed number of dimensions that represent each token in vector space.
| Model | Vocabulary Size | Embedding Dimension |
|---|---|---|
| GPT-2 | 50,257 | 768 |
| GPT-3 | 50,257 | 12,288 |
| GPT-4 (approx.) | ~100,000 | 16,384 |
This means GPT maintains a huge embedding matrix, where each row corresponds to a token and each column represents a feature of that token.
For example, GPT-3’s embedding layer alone contains roughly 617 million parameters (50,257 × 12,288).
🧠 Example: Creating an Embedding Layer in PyTorch
1import torch
2
3input_ids = torch.tensor([2, 3, 5, 1])
4
5vocab_size = 6
6output_dim = 3
7
8torch.manual_seed(123) #Ensures reproducibility — the random numbers used to initialize the embeddings will be the same every time you run the code.
9embedding_layer = torch.nn.Embedding(vocab_size, output_dim)
10
11print("Embedding weights:\n", embedding_layer.weight)
12print("\nEmbedded output:\n", embedding_layer(input_ids))
13# PyTorch’s Embedding layer does not care about the indices of your input tensor.
14# It only uses the values inside that tensor.
**NOTE:**
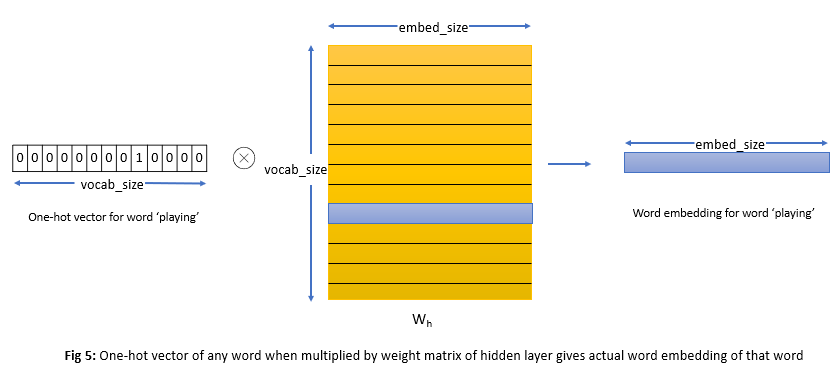
The embedding layer and a neural network linear layer are conceptually similar — both use a weight matrix to map inputs to outputs.
However, the difference lies in how they handle input data.
In a normal linear layer, if you pass a one-hot encoded vector (mostly zeros and one ‘1’), the layer multiplies the entire vector with the weight matrix. This means it performs many unnecessary multiplications with zeros, which don’t affect the final result but still consume computation.
The embedding layer avoids this inefficiency. Instead of multiplying, it directly looks up the corresponding row in the weight matrix using the token ID. For example, if the token ID is 3, it simply returns the 3rd row of the matrix as the embedding vector.
So, the embedding layer gives the same result as a linear layer would with a one-hot input — but it’s much faster and more efficient, because it skips all the zero multiplications and directly retrieves the needed vector.
🧮 How Token Embeddings Are Created
🧩 Step 1 — Initialize the Embedding Matrix
An embedding matrix is created with random values.
Its shape is [vocab_size, embedding_dim], where each row corresponds to a token and each column represents one of its dimensions.
🧩 Step 2 — Convert Token IDs to Embeddings
When text is tokenized, each token is assigned an ID (like [102, 204, 501]).
The embedding layer takes these IDs and looks up the corresponding rows from the embedding matrix to get their vector representations.
This lookup replaces the need for one-hot multiplication and is much more efficient.
🧩 Step 3 — Train and Optimize the Embeddings
During model training (like next-word prediction in GPT), the embeddings are updated through backpropagation.
Only the rows corresponding to the tokens in the current batch are adjusted.
Over many iterations, the model learns to adjust these vectors so that words appearing in similar contexts (like “cat” and “dog”) have similar embeddings, while unrelated words (like “apple”) move further apart in vector space.
🧩 Step 4 — Use Embeddings as Model Input
Once trained, these optimized vectors become the input to the transformer layers of the LLM.
Each embedding now carries meaningful numerical patterns that represent word relationships, semantics, and context.
✅ Summary
- The embedding layer starts with random weights.
- During training, these weights are optimized based on the model’s learning objective.
- The result is a dense vector space where similar words are close and different words are far apart — forming the foundation of understanding for large language models.